Trinity: Brachistochrone Problem;Banach-Tarski Paradox;Basel Problem

We are back with continuation on our A-Z series. We’ve got three interesting topic to write about today and rather than writing all of them in details, the actual mathematical solutions are well beyond our scope, we’ll provide you the insights of the problems, its history and give you as much links as possible that can help you better understand it.

The Brachistochrone

This is one of the very famous problem in history of maths(Calculus Variation) which is named after by such a complicated word. “Brachistochrone” is a Greek word for the shortest time. It is based on the question that was posed by Johann Bernoulli in 17th century.

The question was, “If you imagine a ramp that joins two points A and B and let a ball move through it under the influence of gravity, what path leads the ball in the least amount of time.” It may a parabolic path or arc of a circle or a straight path or may even be some other random curve.

This is a interesting question if you think about it; you want the path to be short(something like a straight line) but you want the ball to get going fast which requires steepness that adds length to you path. Somewhere between length and steepness you need to find a balance.

Bernoulli posed this problem as a problem to the mathematical world at that time to Issac Newton, Leibniz, his brother Jacob Bernoulli and others. Bernoulli knew he had  a clever approach to this problem which relates with Fermat’s Principle of least time and Snell’s law.

As it turns out the curve that yields shortest path is Cyclonic curve(or cycloid). It is a curve traced by a fixed point on the circumference of a circular wheel as the wheel rolls along a straight line without slippage. Now there are many solutions available to the problem.

The links to details and geometrical solutions are given below:

For Detailed background on the problem Click here

For Mark Levis modern twist on solution Click here

For the equation of Cycloid Click here

For Fermat’s Principle of least time Click here

 

Banach Traski Paradox

The Banach-Tarski paradox in  a nutshell states that since an infinite number of points can be found in and make up a finite shape, then that would mean if you rearrange that infinite amount of points, you could make a larger or smaller things as well as different shaped object from the original one that means making duplicating or making new object from the previous one.

Well, it’s counter-intuitive in the real world, but you may find that when you look at it as playing around with infinities, it makes sense. You know what the paradox basically says – that you can split a ball into two balls without losing any thing from original ball.

Watch this Vsauce video about it; and it will make sense: Here

 

Basel’s Problem

Basel’s Problem is a problem related to convergence of an infinite series in Number Theory. It was posed by Mengoli in 1644 which stood as unsolvable problem for about 100 years and was finally solved by Euler.

The question is what does this sum converges into.

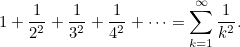First of all this is not like our Geometrical series with ratio; -1<r<1. We cannot even tell if this series converges. As it turns out this sum converges; and it converges into an interesting value.

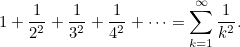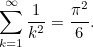Did you see that? The π in the answer; How did it come? Does not that only come with circles? Why does it even comes with infinite sums? Isn’t π a lonely-irrational and unreachable number? Well it isn’t! See how it emerges with infinities.

The solution to this problem is really very hard;But some of the links for help are below:

Solution to Basel’s Problem Here

Now you see that mathematics is a beautiful, elegant, and is a creative discipline. That alone is the fundamental drive and spirit that turns inquisitive grade school students into our future mathematicians, scientists, engineers, and other quantitative problem solvers. These puzzles and paradoxes prove the point.

Note: This series is intended to give viewer the feel for paradoxes; interesting puzzles and problems from the history till now. Links and sites are included rather than detailed analysis itself. Apart from this regular posts will be published every Saturday as usual.